Resolution. The whole truth
A small guide to breaking the spiral of misunderstandings, misinterpretations and errors about the resolution of images intended for printing. Finally.
By Lorenzo Capitani | On PRINTlovers 102
But are we still here writing about the resolution of images intended for printing when, by now, shooting quality, capture quality, network speed and storage space are no longer an issue? Any device today produces very large, quality images by default. Yet there is always an image that is too small (or too big), taken who knows where, perhaps downloaded from the Internet, from some social networking site, passed via WhatsApp, and ended up in some PDF for printing.
But why does image resolution, which should be one of the fundamental aspects of graphics and printing, continue to generate misunderstandings, misinterpretations and errors?
The first reason for this confusion is to be found, before the technical aspects, in an uncertain terminology that cannot be eliminated, which creates ambiguity and endlessly propagates dangerous simplifications. First of all, what is the concept of high and low resolution? High or low in relation to what? If not the unit of measurement, at least a term of comparison. And let it not be said that high and low par excellence refer to the fateful 300 and 72 DPI. Nothing could be more wrong, even if people continue to say (and think) so. Let us try to clarify once and for all.
Pixels per Inch
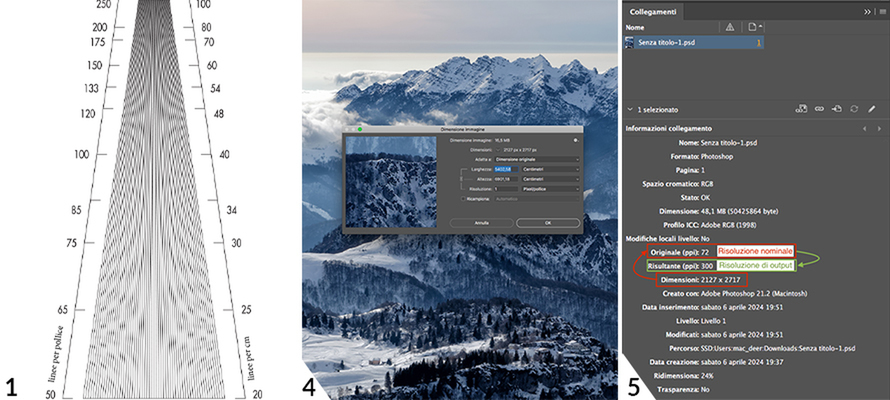
Let's start with DPI. The recurring mantra is that images for printing should be at 300 DPI, i.e. 300 dots per inch (Dots Per Inch) or 300 dots of ink (or toner) per inch. But we supply files, which are not measured in ink dots. As Marco Olivotto writes in his excellent book Understanding Colour, it is like saying, "a bucket of water with the capacity of 10 amperes: the ability is measured in litres, cubic centimetres or other units of measurement suitable for the purpose, but not using the unit of measurement of electric current. DPIs refer to inkjet or laser printing systems and have nothing to do with the image per se. They are a feature of the printer, so let's leave them where they belong.” More correctly, we should speak of PPI or Pixels Per Inch. Of course, PPI becomes DPI when printing offset or digitally, but this results from a downstream transformation that is not our responsibility. Complicating matters then is a third unit of measurement, the LPI or Lines Per Inch, which measures the lines of a typographic screen: the more lines there are in an inch, the finer the reproduction in print will be. There are different lineations depending on the printing technique: the higher the lineation, the higher the print quality. But even in this case, we may as well forget about lineation for image delivery.
To sum up, PPI, DPI, and LPI are all three units of measurement that represent linear density per inch, i.e., how many 'objects' we find in one inch, which equals 2.54 cm. We are only interested in PPI. It is no coincidence that in Photoshop, image sizes are measured in pixels per inch, not dots.1,2
Physical resolution
However, if we look carefully at the table, we realise that all three units measure physical objects which exist in reality (pixels of a monitor, ink dots, lines per inch). In contrast, the pixels of a digital image are not an object but a table of numbers with no physical dimensions. Yet, in both cases, we measure in PPI and speak of resolution. Thus, the two situations should be distinguished by calling nominal resolution the resolution of a digital image (how many rows and columns the image file table has) and physical resolution the resolution of its physical counterpart reproduced by a monitor or in print.3
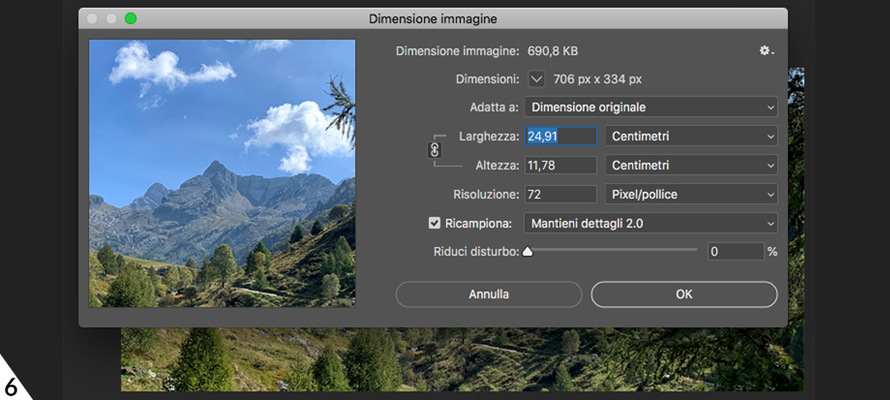
To understand the difference, Marco Olivotto proposes a little experiment. Open any image in Photoshop (e.g. Size 2127 x 2717 pixels with Width 18 cm x Height 23 cm at 300 PPI) and go to the Image/Image Size command; here, uncheck Resample and type 1 in the Resolution field: the values of Width and Height change (becoming 5400 x 6900 cm), but the dimensions in pixels remain unchanged. At this point, save the 1 PPI image as a copy and close it. Re-opening both images, the original and the copy saved at 1 PPI, we notice that they are identical, with no difference.4
This is because the nominal resolution (2127 x 2717 pixels) is nothing more than metadata, a piece of information accompanying the image in the same way as the date and time it was taken: it only tells us the size of the digital image in pixels. It is helpful, but it does not affect the appearance of what we see. Why, then, specify the nominal resolution? A digital image should be represented to be visible, and to represent it, we need a medium, a monitor, or a sheet of paper, which has its physical resolution expressed in PPI. The image of the experiment on a 96 PPI monitor measures 56.25 x 71.89 cm or 18 x 23 cm at 300 PPI.
Output resolution
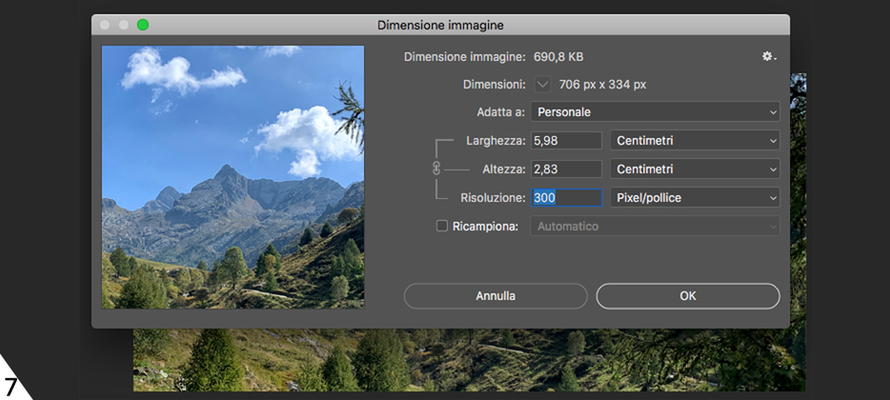
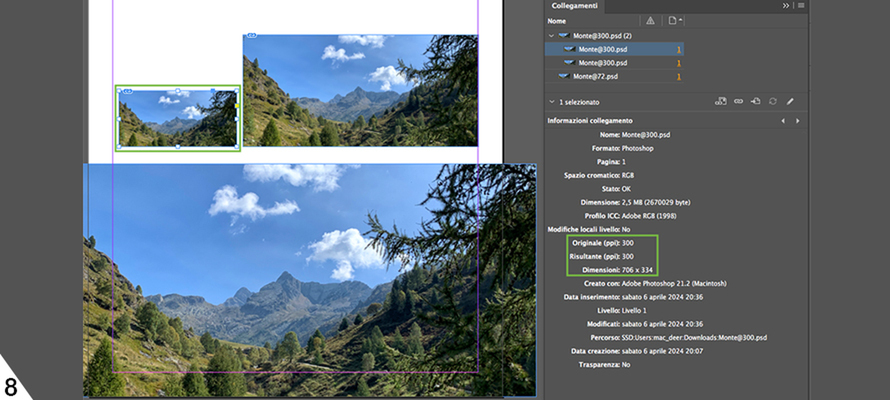
So why is the nominal resolution used, and, above all, when does it come into play, since it is nothing more than a conversion factor that has nothing to do with image quality? For example, in InDesign, when we create a document, we specify the physical dimensions (e.g. 21 x 29.7 cm), but when we import an image, its measurements are taken from its nominal resolution. InDesign in the Links panel calls these measurements Dimensions, like Photoshop, and the nominal resolution Original (PPI). If we resize the image, the Dimensions and the Original resolution remain unchanged. At the same time, what InDesign calls the Resultant (PPI) changes and represents the resolution that that image will have in output, i.e. the output resolution, which is the only parameter that interests us for printing.5
Olivotto again writes that an almost universally known fact is that "images for printing should be prepared at 300 PPI nominal resolution. This is not true: the correct establishment (at least in part) is, if anything, that images should have 300 PPI output resolution when printed.” And that is no slight difference. Let’s now see why.
Print size
We commonly consider an image high resolution when it is close to 300 PPI and low resolution when it is 72. But what happens if we print the same image at 300 and 72 PPI? They might be identical, but the 300 PPI one might look sharp, and the 72 PPI one might not, or vice versa. It all depends on the print size, i.e., the size the image will be when printed: the output resolution depends on this, not the nominal resolution.
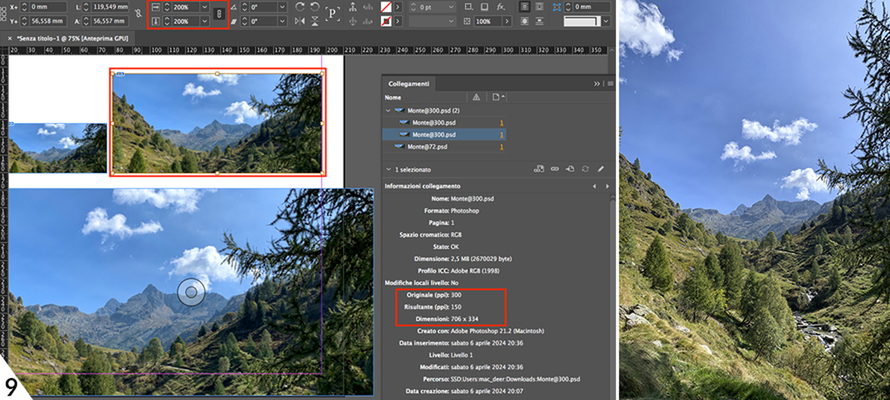
Let's take a 706 x 334-pixel image with a width of 25 cm x height of 12 cm at 72 PPI6: it could be a low resolution as much as a high one; it all depends, in fact, on the size it will be when printed. The 72 PPI alone says nothing. If, for example, I take it to 300 PPI, the nominal resolution will remain the same, but the size will become 6 x 3 cm.7 If I lay it out at 100%, the print will be sharp, but if I lay it out at 200%, it will measure 12 x 6 cm and the output resolution will be halved to 150 PPI and you will see defects and artefacts.8,9
To sum up, only the output resolution needs to be considered in relation to the size of the image when printed. But if I don't have Photoshop at hand to do the conversions, how can I know how much an image will measure at 72 PPI when I take it to 300 PPI? Simply look at the Width and Height that the image has at 72 PPI and divide by 3. Those are roughly the 100% dimensions that the printed image will have. If I make it larger, I will progressively lose quality; if I make it smaller, I will have no problem. If I had a 21 x 10 cm image at 72 PPI intended to be printed, I could reasonably lay it out at 7 x 3 cm without losing quality. It is clear that the fateful 72 PPI is not a low resolution a priori. Yes, but if someone else typesets, how do I know if my image will be suitable for printing? The answer lies in the 300 PPI rule, which is by no means out of the air. If we think of the standard formats of an ideal print where good print quality is required, they are usually close to A4, and the distance from which we view them is between 1.5 and 2 times the diagonal of the sheet. Now, an A4 has a diagonal of about 36 cm, and we observe it from a distance of 54 to 72 cm; if we bring it closer, we can only see part of it; if we move it further away, we can hardly read it.
Viewing distance
There is an empirical formula that allows us to calculate the minimum output resolution in PPI knowing the viewing distance in centimetres:
PPI = 8.733 / viewing distance (in cm)
If we calculate the average between the two indicated limiting distances (54 and 72 cm) for an A4 format, we obtain approximately 60 cm, which, brought into our formula, gives us the following:
8.733/60 = 146 PPI
300 PPI is more than double, so we have a very wide margin: in this case, an output resolution well below 300 PPI would be sufficient to obtain a good print. If, however, we halve the A4, an A5 sheet has a diagonal of 25.8 cm, and we look at it from a distance of about 40 cm (1.5 x 25.8 = 38.7 cm), applying the above formula, we obtain 8.733 / 40 = 349.5 PPI: with 300 PPI we are below this limit. It seems a paradox, but a print requires a higher output resolution, the smaller it is. On the other hand, if we look at a 3 x 6 m poster that will reasonably be seen from 10 m away, the formula gives an output resolution of 8.733/1000 = 9 PPI; rounding up to 20 PPI, we will be fine with the print. It is no coincidence that the print screen of a poster can be seen with the naked eye when you get close; that of a magazine, on the other hand, requires a loupe. In conclusion, it is only possible to establish an optimal output resolution by knowing the distance from which we will observe the print. 300 PPI is also used because it is a functional measure to obtain sufficient output resolution for a high-quality print (with all the above distinctions) without producing too large a file that could slow down printing processes or take up too much storage space.
So, next time, let's look at an image's physical resolution and derive its output resolution according to its print size and type. And, please, no more talk of DPI.
By Lorenzo Capitani | On PRINTlovers 102
But are we still here writing about the resolution of images intended for printing when, by now, shooting quality, capture quality, network speed and storage space are no longer an issue? Any device today produces very large, quality images by default. Yet there is always an image that is too small (or too big), taken who knows where, perhaps downloaded from the Internet, from some social networking site, passed via WhatsApp, and ended up in some PDF for printing.
But why does image resolution, which should be one of the fundamental aspects of graphics and printing, continue to generate misunderstandings, misinterpretations and errors?
The first reason for this confusion is to be found, before the technical aspects, in an uncertain terminology that cannot be eliminated, which creates ambiguity and endlessly propagates dangerous simplifications. First of all, what is the concept of high and low resolution? High or low in relation to what? If not the unit of measurement, at least a term of comparison. And let it not be said that high and low par excellence refer to the fateful 300 and 72 DPI. Nothing could be more wrong, even if people continue to say (and think) so. Let us try to clarify once and for all.
Pixels per Inch
Let's start with DPI. The recurring mantra is that images for printing should be at 300 DPI, i.e. 300 dots per inch (Dots Per Inch) or 300 dots of ink (or toner) per inch. But we supply files, which are not measured in ink dots. As Marco Olivotto writes in his excellent book Understanding Colour, it is like saying, "a bucket of water with the capacity of 10 amperes: the ability is measured in litres, cubic centimetres or other units of measurement suitable for the purpose, but not using the unit of measurement of electric current. DPIs refer to inkjet or laser printing systems and have nothing to do with the image per se. They are a feature of the printer, so let's leave them where they belong.” More correctly, we should speak of PPI or Pixels Per Inch. Of course, PPI becomes DPI when printing offset or digitally, but this results from a downstream transformation that is not our responsibility. Complicating matters then is a third unit of measurement, the LPI or Lines Per Inch, which measures the lines of a typographic screen: the more lines there are in an inch, the finer the reproduction in print will be. There are different lineations depending on the printing technique: the higher the lineation, the higher the print quality. But even in this case, we may as well forget about lineation for image delivery.
To sum up, PPI, DPI, and LPI are all three units of measurement that represent linear density per inch, i.e., how many 'objects' we find in one inch, which equals 2.54 cm. We are only interested in PPI. It is no coincidence that in Photoshop, image sizes are measured in pixels per inch, not dots.1,2
Physical resolution
However, if we look carefully at the table, we realise that all three units measure physical objects which exist in reality (pixels of a monitor, ink dots, lines per inch). In contrast, the pixels of a digital image are not an object but a table of numbers with no physical dimensions. Yet, in both cases, we measure in PPI and speak of resolution. Thus, the two situations should be distinguished by calling nominal resolution the resolution of a digital image (how many rows and columns the image file table has) and physical resolution the resolution of its physical counterpart reproduced by a monitor or in print.3
To understand the difference, Marco Olivotto proposes a little experiment. Open any image in Photoshop (e.g. Size 2127 x 2717 pixels with Width 18 cm x Height 23 cm at 300 PPI) and go to the Image/Image Size command; here, uncheck Resample and type 1 in the Resolution field: the values of Width and Height change (becoming 5400 x 6900 cm), but the dimensions in pixels remain unchanged. At this point, save the 1 PPI image as a copy and close it. Re-opening both images, the original and the copy saved at 1 PPI, we notice that they are identical, with no difference.4
This is because the nominal resolution (2127 x 2717 pixels) is nothing more than metadata, a piece of information accompanying the image in the same way as the date and time it was taken: it only tells us the size of the digital image in pixels. It is helpful, but it does not affect the appearance of what we see. Why, then, specify the nominal resolution? A digital image should be represented to be visible, and to represent it, we need a medium, a monitor, or a sheet of paper, which has its physical resolution expressed in PPI. The image of the experiment on a 96 PPI monitor measures 56.25 x 71.89 cm or 18 x 23 cm at 300 PPI.
Output resolution
So why is the nominal resolution used, and, above all, when does it come into play, since it is nothing more than a conversion factor that has nothing to do with image quality? For example, in InDesign, when we create a document, we specify the physical dimensions (e.g. 21 x 29.7 cm), but when we import an image, its measurements are taken from its nominal resolution. InDesign in the Links panel calls these measurements Dimensions, like Photoshop, and the nominal resolution Original (PPI). If we resize the image, the Dimensions and the Original resolution remain unchanged. At the same time, what InDesign calls the Resultant (PPI) changes and represents the resolution that that image will have in output, i.e. the output resolution, which is the only parameter that interests us for printing.5
Olivotto again writes that an almost universally known fact is that "images for printing should be prepared at 300 PPI nominal resolution. This is not true: the correct establishment (at least in part) is, if anything, that images should have 300 PPI output resolution when printed.” And that is no slight difference. Let’s now see why.
Print size
We commonly consider an image high resolution when it is close to 300 PPI and low resolution when it is 72. But what happens if we print the same image at 300 and 72 PPI? They might be identical, but the 300 PPI one might look sharp, and the 72 PPI one might not, or vice versa. It all depends on the print size, i.e., the size the image will be when printed: the output resolution depends on this, not the nominal resolution.
Let's take a 706 x 334-pixel image with a width of 25 cm x height of 12 cm at 72 PPI6: it could be a low resolution as much as a high one; it all depends, in fact, on the size it will be when printed. The 72 PPI alone says nothing. If, for example, I take it to 300 PPI, the nominal resolution will remain the same, but the size will become 6 x 3 cm.7 If I lay it out at 100%, the print will be sharp, but if I lay it out at 200%, it will measure 12 x 6 cm and the output resolution will be halved to 150 PPI and you will see defects and artefacts.8,9
To sum up, only the output resolution needs to be considered in relation to the size of the image when printed. But if I don't have Photoshop at hand to do the conversions, how can I know how much an image will measure at 72 PPI when I take it to 300 PPI? Simply look at the Width and Height that the image has at 72 PPI and divide by 3. Those are roughly the 100% dimensions that the printed image will have. If I make it larger, I will progressively lose quality; if I make it smaller, I will have no problem. If I had a 21 x 10 cm image at 72 PPI intended to be printed, I could reasonably lay it out at 7 x 3 cm without losing quality. It is clear that the fateful 72 PPI is not a low resolution a priori. Yes, but if someone else typesets, how do I know if my image will be suitable for printing? The answer lies in the 300 PPI rule, which is by no means out of the air. If we think of the standard formats of an ideal print where good print quality is required, they are usually close to A4, and the distance from which we view them is between 1.5 and 2 times the diagonal of the sheet. Now, an A4 has a diagonal of about 36 cm, and we observe it from a distance of 54 to 72 cm; if we bring it closer, we can only see part of it; if we move it further away, we can hardly read it.
Viewing distance
There is an empirical formula that allows us to calculate the minimum output resolution in PPI knowing the viewing distance in centimetres:
PPI = 8.733 / viewing distance (in cm)
If we calculate the average between the two indicated limiting distances (54 and 72 cm) for an A4 format, we obtain approximately 60 cm, which, brought into our formula, gives us the following:
8.733/60 = 146 PPI
300 PPI is more than double, so we have a very wide margin: in this case, an output resolution well below 300 PPI would be sufficient to obtain a good print. If, however, we halve the A4, an A5 sheet has a diagonal of 25.8 cm, and we look at it from a distance of about 40 cm (1.5 x 25.8 = 38.7 cm), applying the above formula, we obtain 8.733 / 40 = 349.5 PPI: with 300 PPI we are below this limit. It seems a paradox, but a print requires a higher output resolution, the smaller it is. On the other hand, if we look at a 3 x 6 m poster that will reasonably be seen from 10 m away, the formula gives an output resolution of 8.733/1000 = 9 PPI; rounding up to 20 PPI, we will be fine with the print. It is no coincidence that the print screen of a poster can be seen with the naked eye when you get close; that of a magazine, on the other hand, requires a loupe. In conclusion, it is only possible to establish an optimal output resolution by knowing the distance from which we will observe the print. 300 PPI is also used because it is a functional measure to obtain sufficient output resolution for a high-quality print (with all the above distinctions) without producing too large a file that could slow down printing processes or take up too much storage space.
So, next time, let's look at an image's physical resolution and derive its output resolution according to its print size and type. And, please, no more talk of DPI.